Chapter 3 - Z-transform
Direct z-transform, convergence, finite-duration sequences, infinite-duration sequence, ROC, inverse z-transform.
Direct z-transform
Let's say we have the sequence:
$$x(n)=\begin{bmatrix}\cdots&x_{-1}&\underline{x_{-0}}&x_1&\cdots\end{bmatrix}$$
then the z-transform of the sequence is a power series in z:
$$X(z)=\cdots+x_{-1}z^1+x_{-0}z^0+x_1z^{-1}+\cdots $$
We can write the power series as:
$$X(z)\equiv\sum_{n=-\infty}^{\infty}x(n)z^{-n}$$
Then we write the relationship between the transform pair:
$$x(n) \overset{z}\longleftrightarrow X(z)$$
The z-transform `X(z)` is a complex function of a complex variable `z`.
Convergence of `X(z)`
The region of convergence (ROC) of `X(z)` is:
$$\text{ROC:All }z\in\mathbb{C}\text{ for which }|X(z)|<\infty $$
and we say that the z-transform only exists inside its ROC.
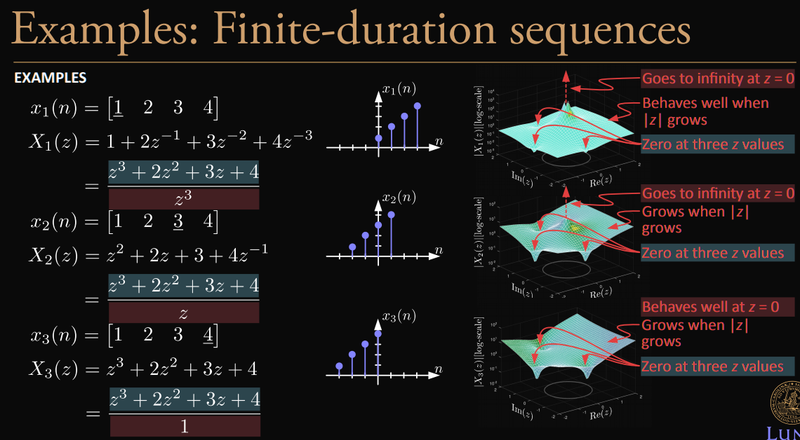
Example: Finite-duration sequences
Example: Infinite-duration sequence
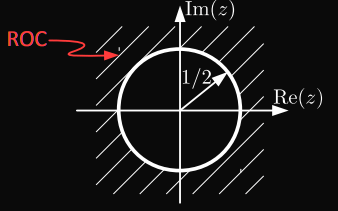
Let `x(n)` be the sequence: `x(n) = 0.5^nu(n)`.
The z-transform is:
$$
\begin{split}
X(z) &= \sum_{n=-\infty}^\infty x(n)z^{-n} \\
= \sum_{n=0}^\infty 0.5^n z^{-n} &= \sum_{n=0}^\infty (0.5z^{-1})^n
\end{split}
$$
This is a geometric series which evaluates to:
$$X(z) = \frac{1}{1 - 0.5z^{-1}}\text{ for }|0.5z^{-1}|<1$$
The convergence requirement for the geometric sum helps us find the ROC:
$$
\begin{split}
|\frac{1}{2}z^{-1}|<1 \iff \frac{1}{2}|z^{-1}|<1 \\
\iff \frac{1}{2|z|} < 1 \iff |z| > \frac{1}{2}
\end{split}
$$
Since z is complex number we can illustrate this as